Hieronder volgen de wiskundige afleidingen van gulden snede, rij van Fibonacci en Golden Spiral. Dit is leuk als achtergrond informatie maar voor fotografie niet direct te gebruiken. Hoe je de gulden snede (en regel van derden) kunt gebruiken in de fotografie lees je in dit uitgebreide artikel: www.johanvanderwielen.nl/werken-met-de-gulden-snedeof-regel-van-derden
Wiskundige afleiding van de Gulden Snede en Golden Ratio
Let op… Johan is wiskundige van huis uit, nu word ik even lekker freaky.
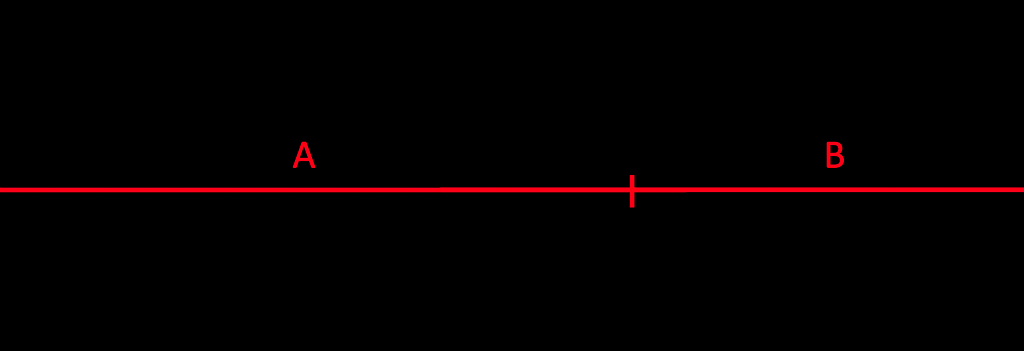
De gulden snede, of de ‘perfecte verhouding’, is wiskundig te berekenen. We beginnen met een lijnstuk welke we in twee verdelen, lengtes ![]() en
en ![]() .
.
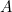 en
en 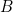 waarbij we de verhouding tussen
waarbij we de verhouding tussen 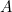 en
en 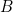 gelijk willen hebben als de verhouding tussen
gelijk willen hebben als de verhouding tussen 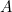 en het hele lijnstuk
en het hele lijnstuk 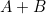 .
.De verhouding tussen de delen ![]() en
en ![]() en het hele lijnstuk
en het hele lijnstuk ![]() kun je wiskundig als volgt beschrijven:
kun je wiskundig als volgt beschrijven:
![]()
Nu komt de truc van het omrekenen. Op zich zijn we niet geïnteresseerd in ![]() of
of ![]() zelf maar juist in de verhouding tussen beiden. Met andere woorden, we kunnen
zelf maar juist in de verhouding tussen beiden. Met andere woorden, we kunnen ![]() het beste opschrijven als een nieuw getal, hiervoor wordt meestal de Griekse letter Phi of
het beste opschrijven als een nieuw getal, hiervoor wordt meestal de Griekse letter Phi of ![]() gebruikt. Je krijgt dan:
gebruikt. Je krijgt dan:
![]()
Als je dat in de eerste formule invult krijg je: ![]()
Door nu verder te gaan delen kom je op: ![]()
Omdat ![]() geldt ook dat
geldt ook dat ![]()
Als we dat weer invullen krijgen we: ![]()
We hebben nu een vergelijking met één onbekende, en uit de wiskunde weet je misschien nog wel dat dat op te lossen is. Hieronder de oplossing door eerst links en rechts met ![]() te vermenigvuldigen.
te vermenigvuldigen.
![]()
![]()
We hebben nu een kwadratische vergelijking die op te lossen is door middel van de volgende algemene formule: ![]()
Waarbij ![]() dan is uit te rekenen als volgt:
dan is uit te rekenen als volgt: ![]()
Als we dit bepalen in onze eigen vergelijking waarbij ![]() dan
dan ![]() is, dan is
is, dan is ![]() ,
, ![]() en
en ![]() . En dus:
. En dus:
![]()
Dat betekent dat er 2 oplossingen zijn voor ![]() . Echter is
. Echter is ![]() dus één van de oplossingen zal negatief zijn en dat is in essentie niet mogelijk in ons probleem. Dus blijft over:
dus één van de oplossingen zal negatief zijn en dat is in essentie niet mogelijk in ons probleem. Dus blijft over:
![]()
Met andere woorden, ![]() is ca.
is ca. ![]() zo groot als
zo groot als ![]() en tegelijk is
en tegelijk is ![]() ca.
ca. ![]() zo groot als
zo groot als ![]() . Het getal
. Het getal ![]() Wordt de gouden ratio genoemd. Het getal heeft een oneindige aantal decimalen maar repeteert niet. Het is daarmee ‘irrationeel’, net als
Wordt de gouden ratio genoemd. Het getal heeft een oneindige aantal decimalen maar repeteert niet. Het is daarmee ‘irrationeel’, net als ![]() .
.
Als we nu teruggaan naar het lijnstuk dan willen we eigenlijk wel weten wat de relatieve groottes zijn van ![]() en
en ![]() . Dus stel dat
. Dus stel dat ![]() gelijk is aan
gelijk is aan ![]() dan kunnen we
dan kunnen we ![]() en
en ![]() als volgt berekenen:
als volgt berekenen:
![]()
![]()
Met andere woorden. Als ![]() het hele lijnstuk is, zeg
het hele lijnstuk is, zeg ![]() , dan ligt
, dan ligt ![]() op ca.
op ca. ![]() en
en ![]() op ca.
op ca. ![]() . Je ziet dat deze waarden in de buurt komen van de
. Je ziet dat deze waarden in de buurt komen van de ![]() en
en ![]() van de regel van derden maar net niet helemaal. De regel van derden is een vereenvoudiging van de gulden snede en makkelijker mee te werken.
van de regel van derden maar net niet helemaal. De regel van derden is een vereenvoudiging van de gulden snede en makkelijker mee te werken.
Relatie tussen de Golden Ratio en de Fibonacci reeks…
Er is een belangrijke relatie tussen de Golden Ratio ![]() en de reeks van Fibonacci. Maar eerst wat is de Fibonacci reeks ook weer. Het is een reeks van getallen waarbij het volgende getal wordt gevormd uit de som tussen de vorige twee. Laten we beginnen met de getallen
en de reeks van Fibonacci. Maar eerst wat is de Fibonacci reeks ook weer. Het is een reeks van getallen waarbij het volgende getal wordt gevormd uit de som tussen de vorige twee. Laten we beginnen met de getallen ![]() en
en ![]() . Als je die optelt krijg je wederom
. Als je die optelt krijg je wederom ![]() maar als je nu de laatste twee getallen in de reeks
maar als je nu de laatste twee getallen in de reeks ![]() optelt krijg je
optelt krijg je ![]() . De reeks wordt nu:
. De reeks wordt nu:
![]()
In formule kun je het ![]() getal in de Fibonacci reeks als volgt schrijven:
getal in de Fibonacci reeks als volgt schrijven:
![]()
Tussen iedere twee opeenvolgende getallen in de Fibonacci reeks kun je de verhouding berekenen:
![]()
We kunnen nu de reeks van verhoudingen berekenen:
![]()
Je ziet dat met 3 cijfers achter de komma de verhouding tussen ![]() heel snel richting
heel snel richting ![]() , de Golden Ratio gaat. Hoe groter
, de Golden Ratio gaat. Hoe groter ![]() , hoe beter de benadering voor
, hoe beter de benadering voor ![]() . Dat is ook wel logisch, immers…
. Dat is ook wel logisch, immers…
![]()
Neem ![]() en
en ![]() en je krijgt (zie hierboven bij de afleiding van de Gulden Snede):
en je krijgt (zie hierboven bij de afleiding van de Gulden Snede):
![]()
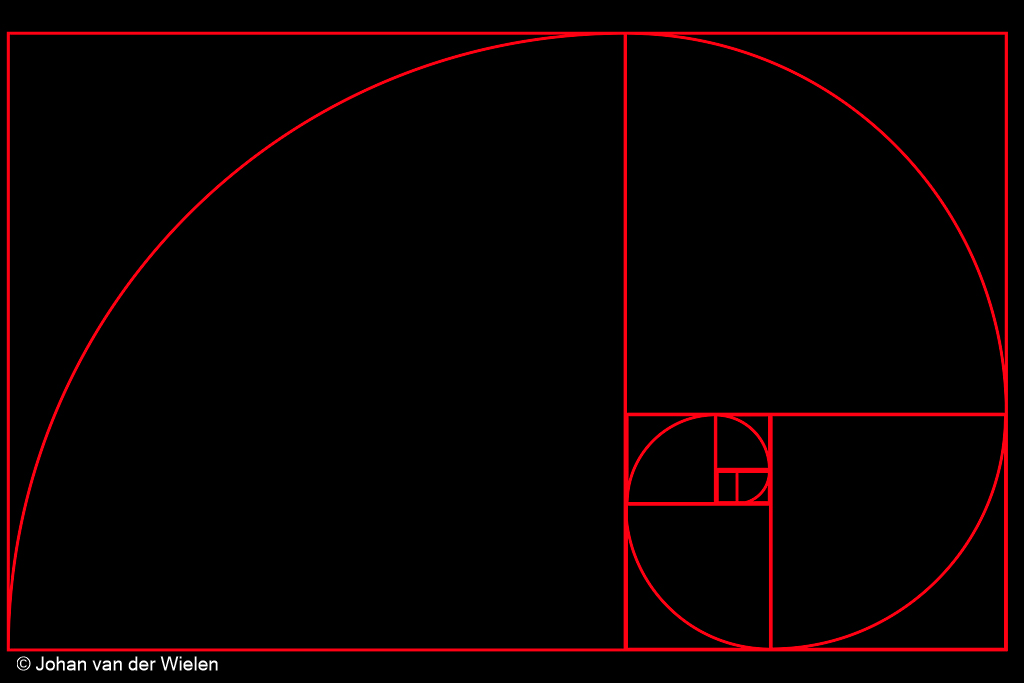
De Golden Spiral
Je hebt misschien wel eens gehoord van de ‘Golden Spiral‘. Het is bijvoorbeeld één van de crop overlays bij de meeste foto nabewerkingssoftware pakketten. Maar waar komt die spiraal vandaan?
We beginnen weer met de verhoudingen ![]() en
en ![]() conform de ‘Golden Ratio‘.
conform de ‘Golden Ratio‘.
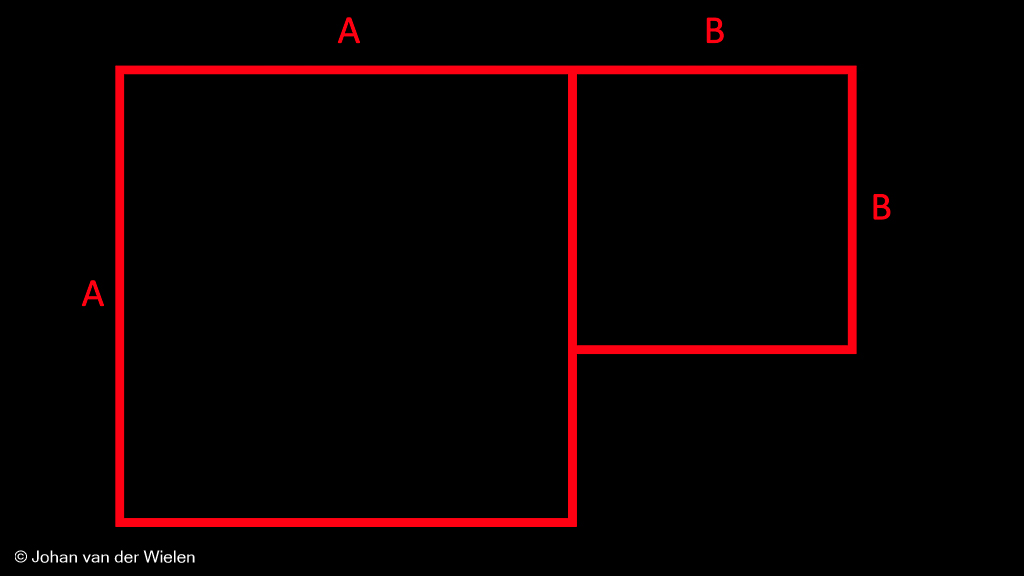
Wat opvalt is dat vierkant met lengte ![]() precies onder vierkant met lengte
precies onder vierkant met lengte ![]() valt. Het lijkt erop dat
valt. Het lijkt erop dat ![]() . Is dit verklaarbaar? Laten we een paar vergelijkingen er weer bij pakken:
. Is dit verklaarbaar? Laten we een paar vergelijkingen er weer bij pakken:
![]()
Omdat we dezelfde verhouding ![]() hebben gebruikt voor de verhouding tussen
hebben gebruikt voor de verhouding tussen ![]() en
en ![]() geldt dus ook:
geldt dus ook:
![]()
Omdat deze vier beschreven verhoudingen allemaal gelijk zijn aan ![]() kun je stellen dat:
kun je stellen dat:
![]()
Dan is het dus ook logisch dat vierkant met lengte ![]() precies in het lege gat onder het vierkant met lengte
precies in het lege gat onder het vierkant met lengte ![]() valt.
valt.
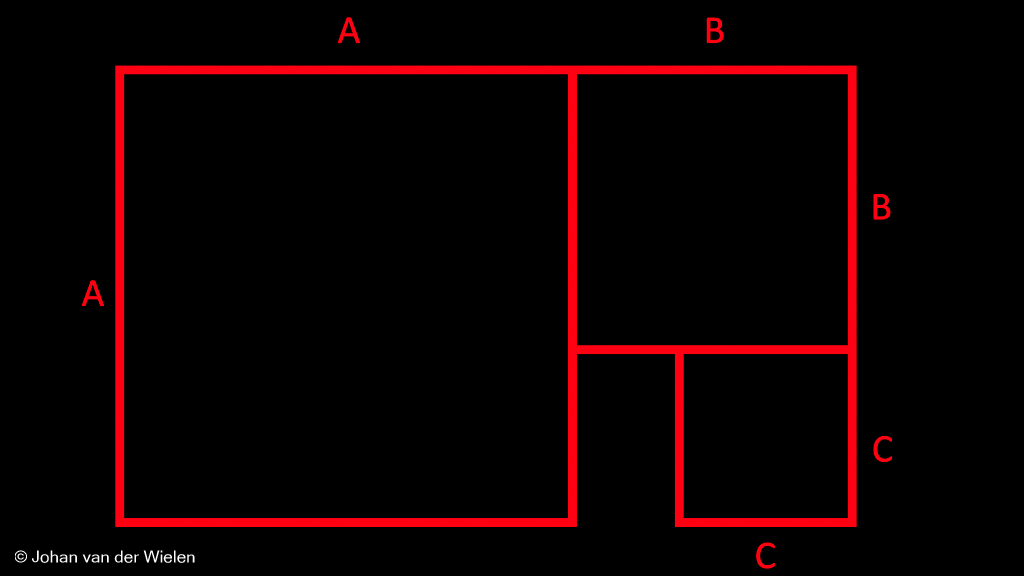
Op dezelfde wijze kunnen we natuurlijk doorgaan:
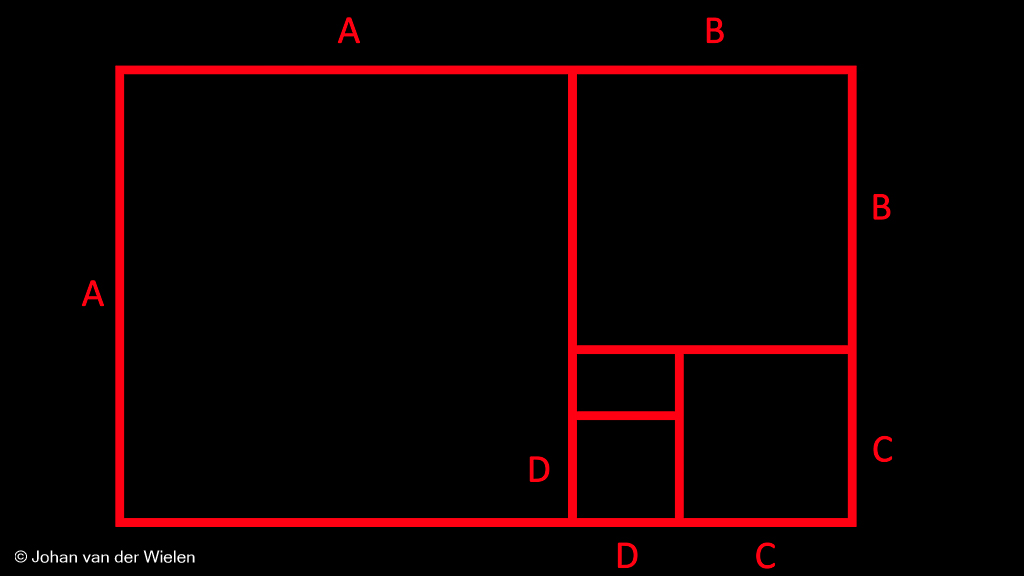
Je ziet dat we dit proces in essentie oneindig kunnen herhalen. In het lege gat tussen de vier vierkanten kunnen we nu een weer kleiner vierkant plaatsen met lengte ![]() zodanig dat
zodanig dat ![]() , etc. etc.
, etc. etc.
In ieder vierkant kunnen we een kwart cirkel tekenen met de straal van het betreffende vierkant. Deze kunnen we laten aansluiten… wat we dan krijgen is:


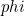 , dus
, dus 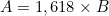 .
.
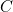 waarvoor geldt dat
waarvoor geldt dat 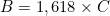 of
of 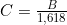 .
.
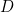 waarvoor geldt dat
waarvoor geldt dat 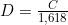 .
.